Luas Daerah Yang Diarsir Adalah Selisih Luas Bangun Datar, Begini Penjelasannya

Luas Daerah Yang Diarsir

Luas daerah yang diarsir adalah selisih luas satu dengan luas lainnya. Sehingga penting untuk memahami rumus luas dari masing-masing bangun datar.

Misalnya saja bisa dengan rumus luas persegi, persegi panjang, segitiga, lingkaran, dan lain sebagainya. Pada dasarnya, tidak ada rumus pasti untuk menghitung luas daerah yang diarsir. Luas daerah yang diarsir adalah hasil yang bisa dihitung dengan banyak rumus.

Luas Daerah Bangun Datar

Bangun datar adalah bidang datar yang dibatasi oleh garis-garis lurus atau lengkung. Bangun datar ini bisa juga disebut sebagai bangunan dua dimensi yang memiliki panjang dan lebar. Sementara bangunan yang lain dibatasi garis lurus dan garis lengkung.

Untuk dapat menghitung luas daerah yang diarsir perlu memahami rumus-rumus dasar dari bangun datar.  Rumus-rumus inilah yang nantinya akan membantu mengetahui luas daerah yang diarsir.

Rumus-Rumus Bangun Datar

Persegi

Bangun datar persegi adalah persegi panjang yang semua sisinya mempunyai panjang yang sama.

• Rumus Luas Persegi = s x s (s²)
• Rumus Keliling Persegi = 4 x s (s adalah sisi)

Persegi Panjang

Bangun datar persegi panjang adalah suatu bangun datar yg memiliki sisi yang berhadapan yang sama panjang dan mempunyai 4 buah titik sudut yang siku-siku.

• Rumus Luas Persegi Panjang = p x l
• Rumus Keliling Persegi Panjang = 2 x (p+l) || p : panjang dan l : lebar

Jajar Genjang

Bangun datar jajar genjang adalah bangun segi empat yang mempunyai sisi sepasang – pasang yang sama panjang dan sejajar. 

• Rumus Luas Jajar Genjang = a x t || a : alas dan t : tinggi
• Rumus Keliling Jajar Genjang = AB + BC + CD + AD

Trapesium

Bangun datar trapesium adalah bangun segi empat yang mempunyai sepasang sisi yang sejajar. 

• Rumus Luas Trapesium = ½ x jumlah sisi sejajar x tinggi
• Rumus Keliling Trapesium = AB + BC + CD + DA

Layang-Layang

Bangun datar layang-layang adalah bangun segi empat yang salah satu diagonalnya dapat memotong tegak lurus dengan sumbu diagonal yang lainnya.

• Rumus Luas Layang-Layang = ½ x d1 x d2 || d : diagonal
• Rumus Keliling Layang-Layang = 2 x (AB + BC)

Segitiga 

Bangun Datar Segitiga adalah bangun datar yg dibentuk oleh 3 buah titik yg titik tersebut tidak segaris.

• Rumus Luas Segitiga = ½ x a x t || a : alas dan t : tinggi
• Rumus Keliling Segitiga = AB + BC + AC

Belah Ketupat

Bangun datar belah ketupat adalah bangun segi empat yang semua sisi-sisinya itu sama panjang dan kedua diagonal belah ketupat saling berpotongan tegak lurus.

• Rumus Luas Belah Ketupat = ½ x di x d2 || d : diagonal
• Rumus Keliling Belah Ketupat = 4 x s || s : sisi

Lingkaran

Bangun datar lingkaran adalah bangun datar yang terbentuk dari himpunan-himpunan yang semua titiknya mengelilingi suatu titik asal dengan jarak yang sama. Jarak itu biasanya dilambangkan dengan r (Radius) atau sering disebut juga jari-jari. 

• Rumus Luas Lingkaran = π x r² (π : 22/7 atau 3.14 dan r : jari-jari)
• Rumus Keliling Lingkaran = π x d (π : 22/7 atau 3.14 dan d : diameter)

Contoh Luas Daerah Yang Diarsir

Perhatikan gambar berikut.

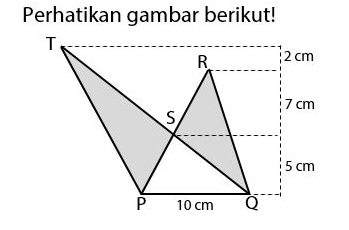
Luas daerah yang diarsir adalah…?

Pembahasan:

Luas daerah yang diarsir terdiri dari dua buah segitiga, yaitu ?PST dan ?QRS. Sehingga, untuk menghitung luas daerah yang diarsir perlumenghitung kedua luas segitiga tersebut terlebih dahulu.

L?PST = L?PQT – L?PQS = ½ × 10 × 14 – ½ × 10 × 5 = 70 – 25 = 45 cm2

L?QRS = L?PQR – L?PQS = ½ × 10 × 12 – ½ × 10 × 5 = 60 – 25 = 35 cm2

Larsir = L?PST + L?QRS = 45 + 35 = 80 cm2

Jadi, luas daerah yang diarsir adalah 80 cm2

Contoh Luas Daerah Yang Diarsir

Perhatikan gambar berikut.

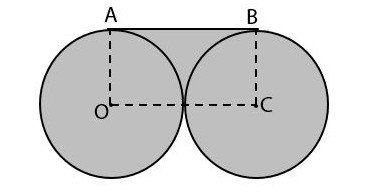
Dua lingkaran dengan pusat O dan C adalah dua lingkaran yang sama. Luas total bangun yang diarsir adalah 329 cm2. Luas persegipanjang OABC adalah ….

A. 231 cm2

B. 129 cm2

C. 98 cm2

D. 68 cm2

Pembahasan:

Luas total daerah yang diarsir sama dengan dua kali ¾ lingkaran dan luas persegi OABC.

Larsir = 2 × ¾ LO + LOABC Larsir = 2( ¾ × π × OA2 ) + (OA × OC) Larsir = 2( ¾ × π × r2 ) + (r × 2r) Larsir = 3/2 × 22?7 × r2 + 2r2 Larsir = 33/7r2 + 2r2 Larsir = 33/7r2 + 14?7r2 Larsir = 47?7r2

Menghitng jari – jari:

329 = 47?7r2 r2 = 7?47 × 329 r2 = 49 r = 7 cm

Menghitung luas OABC:

LOABC = OA × OC = r × 2r = 2r2 = 2 × 72 = 2 × 49 = 98 cm2

(Diambil dari berbagai sumber)